TGhost

Et ces gens voulaient controler les fakes news, ce qui est info ou pas...

Tout est propagande. que ce soit clair.

La France devient/est un regime autoritaire. Yep !

cross-posted from: https://lemmy.dbzer0.com/post/14618292

Le fil de com, sur LinuxFr est interessant,

https://web.archive.org/web/20240216164701/https://www.legalis.net/actualite/orange-condamne-a-650-000-e-pour-non-respect-de-la-licence-gpl/

https://www.zdnet.fr/blogs/l-esprit-libre/non-respect-de-la-licence-gpl-orange-condamne-en-appel-39964312.htm

cross-posted from: https://lemmy.dbzer0.com/post/14618228

LMAO

cross-posted from: https://lemmy.dbzer0.com/post/14618160

Edit 19/02/24 vers les 17h,… : Ce qui est interessant ici, n’est pas le fait divers en lui meme. Ce qui est interessant ici, c’est de voir comment un territoire entier peut s’embraser avec un evenement declencheur (ici le contentieux locatif), dont tout le monde s’en fout. Sur fonds de tensions raciales, veut dire que des locataires “locaux” iraient defendre ce salop, mais juste parce qu’il est noir. Ils doivent partir du postulat qu’il est innocent. Ca craint. Comment on en arrive a une situation, ou le communautarisme prend le pas sur le reste. Ca vient bien de quelque part.

Pour moi on en arrive la, car malheureusement il ya des restes de “colonisations”, d’oppressions, de mepris. Et tant que la “France” n’investira pas dans la paix sociale pour moi rien ne changera.

Je ne suis pas de la bas. A part mes opinions, je connais pas grand chose de la realite de ce territoire.

Apres savoir si la Guadeloupe est stricto francais, je ne peux pas personnellement dire. C’est les populations locales qui peuvent s’exprimer, pas moi.

Bon jai edité, pour que ce soit plus clair, car ca en devient “ridicule”. Demagogie que j’avais dit. Quand je parle de justice de l’homme blanc, bien evidemment que je ne pleure pas cette enflure de proprio, dans cette histoire.

Je parle du territoire en general, sur le long terme, avec juste le titre de l’article en tete pour le coup.

Sur fond de tensions raciales tout pete a la suite dun banal contentieux.

L’evenement n’est que le declencheur, mais pas la matiere de tout cela. En ayant une vue de “dessus” on s’en fout limite de levenement initiateur. Pourquoi ca pete.

Genre une dispute dans un couple toxique, ca part de quelque chose, mais ca balance de maniere desordonnee tout les dossiers, les non dits accumules etc. Jy vois un //. Genre une revolte des banlieues, on ne retient que les jeunes qui cassent sans comprendre l’environnement dans lequel ils evoluent,

etc etc.

Apres accusez de racismes ou que sais je, pas de soucis. Ca fait juste rire.

tax-the-rich.eu

Dans un article du 15 février 2024, nos excellents confrères de Politis donnaient des détails sur les nouveaux équipements que les forces de l'ordre seraient amenées bientôt à balancer aux pieds — ou dans la poire, c'est selon — des manifestants, récalcitrants ou non.

Notamment, Politis évoquait une grenade du fabricant brésilien Condor, la GL-307, une grenade à laquelle les fabricants et les pandores, dans leur jargon, accolent le qualificatif mignon-tout-plein « à effet sonore ». C'est sympa, les effets sonores, ça nous fait penser à Star Wars en THX ou à un mix de Cut Killer, non ?

Politis nous explique d'ailleurs que « selon la documentation de Condor, à une distance de 2 mètres, l’intensité de la grenade de maintien de l’ordre atteint 175 dB ». Ça doit être vachement sympa, comme effet sonore, assurément.

Mais alors, c'est quoi une grenade à « effet sonore » ? Et 175 dB, on imagine que c'est sans doute pas mal beaucoup, mais beaucoup combien ? Difficile en effet de se le représenter. Grenade à effet sonore ?

Le son, ce sont des déplacements d'air qui vont provoquer des variations de pression sur un certains nombre de récepteurs mécaniques situés dans nos esgourdes. Le principe d'une grenade à effet sonore c'est, basiquement, de déplacer une grande quantité d'air quasiment instantanément. Un pétard, quoi. Mais un pétard vénère. En fait, quelques grammes d'un explosif puissant, ça donne un bon son brut pour les truands.

Ce que nos oreilles perçoivent, donc, ce sont les variations de la pression de l'air. On parle de « pression acoustique », en fait une force mécanique, que l'on exprime en « pascals », du nom du scientifique éponyme. Et dans le cas de la déflagration causée par une grenade, la pression de l'air à tendance à exploser, si l'on peut dire. Décibel ?

La perception du son par nos oreilles n'est pas linéaire. Autrement dit, un son que nous percevons deux fois plus fort ne correspondra pas à un doublement de la pression acoustique.

Le seuil inférieur de perception de nos oreilles, c'est 0,00002 pascals, soit 20 micropascals. Une variation dans la pression de l'air très légère, par exemple le bruit émis par les battements d'ailes d'un papillon. Une conversation produit environ 0,006 pascals, soit 6 millipascals, c'est à dire 300 fois plus que les ailes de notre lépidoptère. Un marteau-piqueur, environ 6 pascals, 300 000 fois plus. Le seuil au-delà duquel le son provoque une douleur est situé à environ 20 pascals, de l'ordre d'un million de fois supérieur.

Le seuil au delà duquel le son peut devenir nocif en cas d'exposition répétée, c'est 0,36 pascals, 18 000 fois plus que le seuil inférieur d'audibilité. Plus on s'aventure au-dessus de cette valeur, plus la pression acoustique est susceptible d'endommager notre audition de manière permanente, en clair, de nous rendre irrémédiablement sourds.

Quoi qu'il en soit, on voit que ces valeurs, et surtout leurs ordres de grandeur, sont très éloignés les uns des autres. On passe du micro, du très petit, au million, le très grand. C'est pour cette raison qu'il est d'usage d'utiliser une unité « relative », le décibel, qui décrit mieux la perception du son par nos oreilles humaines. Il définit le rapport entre ce que nous entendons et le seuil inférieur — le papillon — passé dans la fonction de logarithme décimal. Pas d'inquiétude, ce n'est pas si compliqué, cela répond à la formule suivante, où p est la pression acoustique :

décibel = 20 x log(pression_acoustique / 0,00002)

Le décibel, comme le logarithme sur lequel il est basé, met les petites valeurs en avant et amoindrit progressivement les valeurs les plus élevées pour, en quelque sorte, permettre une lecture fondée sur les ordres de grandeur.

C'est ainsi le décibel qui est utilisé lorsque l'on veut décrire l'intensité sonore d'un phénomène, comme dans cette illustration de Sciences et Avenir :

Les décibels sont une unité pratique lorsque l'on parle de notre perception des sons. Il est néanmoins utile de rappeler que, si l'on veut parler des dégâts qu'est susceptible d'engendrer une grenade sur l'audition, c'est bien la pression acoustique qu'il convient d'observer. Car c'est cette pression, cette force exercée par l'onde de choc de l'explosion, qui est à même de déglinguer durablement l'audition de nos concitoyens.

Commençons par tracer un graphique avec, sur l'abscisse (l'axe horizontal), les décibels et la pression acoustique en ordonnée (l'axe vertical), exprimée sur une échelle logarithmique :

On peut voir assez clairement que le rapport entre la pression et l'intensité sonore est constant. La pression acoustique augmente de manière linéaire, traçant une parfaite ligne droite. À peu près au milieu entre la pression provoquée par un avion au décollage et celle engendré par le papillon, on trouvera le seuil de nocivité.

Maintenant, amusons-nous à conserver les mêmes données mais à utiliser une échelle linéaire au lieu d'une échelle logarithmique :

D'un coup, le graphique ne nous raconte plus la même histoire. Exit le papillon, la conversation et même le seuil de nocivité. On ne les voit plus, car ils se confondent avec le "zéro", l'origine de notre graphique. Il ne reste guère que le seuil de douleur, avec ses 20 pascals qui nous feraient presque pitié, perdu tout en bas du graphique. En haut, notre avion au décollage impose sa majesté et survole tout ce beau monde du haut de ses t'as-vu-mes-gros-réacteurs-tiens-200-pascals-dans-ta-face.

Et si on rajoutait la GL-307 sur ce graphique ? Ah, oui, bonne idée ça, regardons ensemble ce que cela pourrait donner :

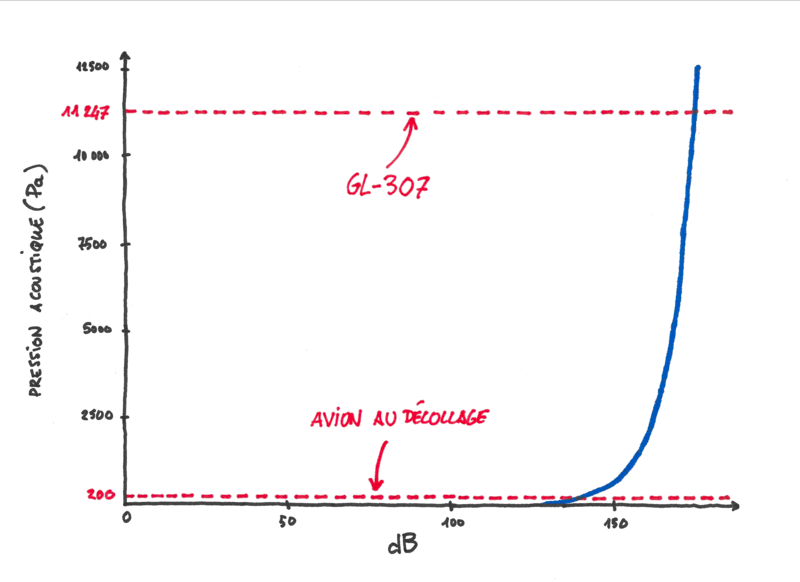
Allez, à la prochaine, on se verra peut-être en manif. Mais pas sûr qu'on s'y entende longtemps.