this post was submitted on 20 Aug 2024
743 points (97.0% liked)
Memes
45670 readers
2050 users here now
Rules:
- Be civil and nice.
- Try not to excessively repost, as a rule of thumb, wait at least 2 months to do it if you have to.
founded 5 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
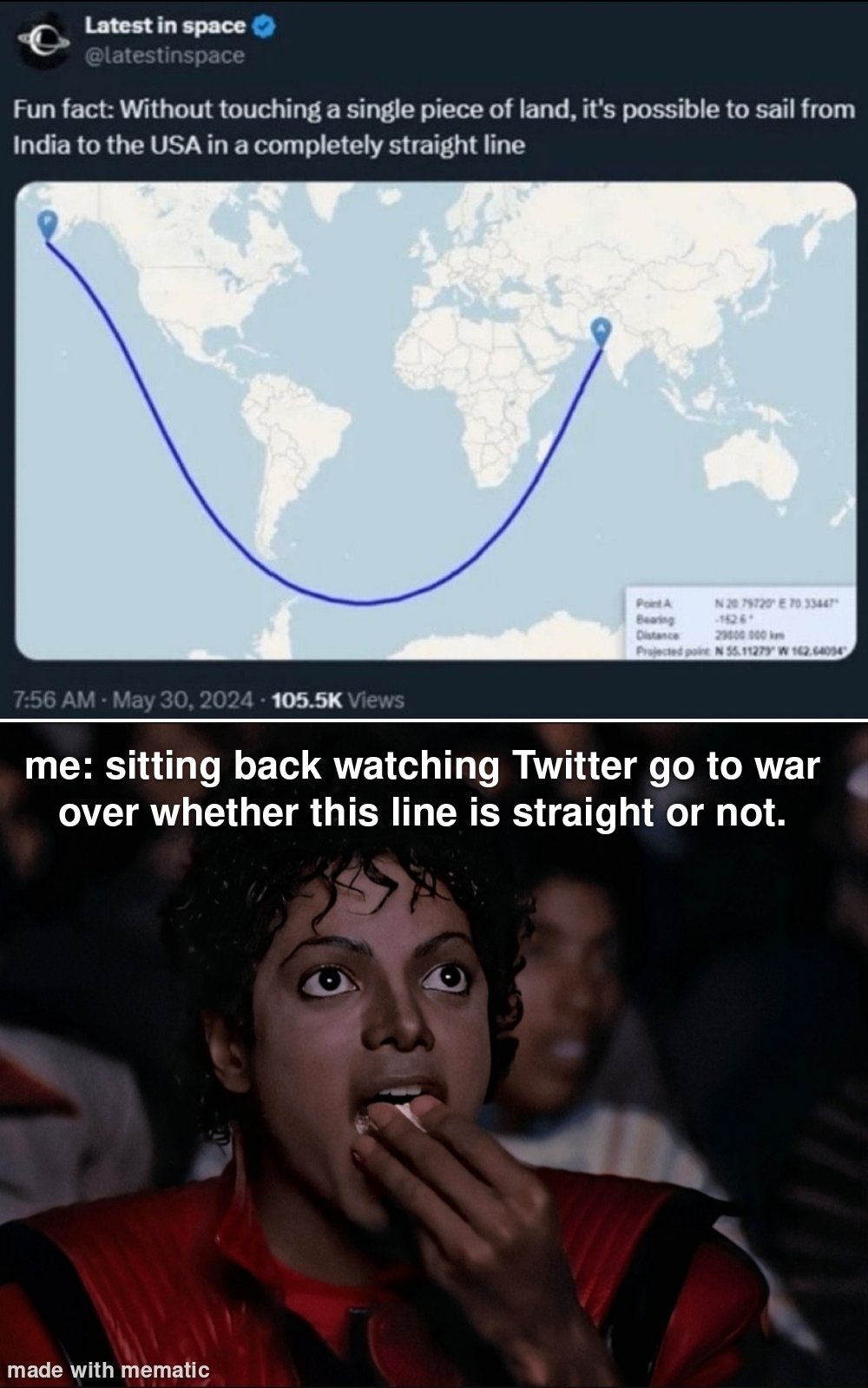
it's a bit of a "spirit of the law vs letter of the law" kind of thing.
technically speaking, you can't have a straight line on a sphere. but, a very important property of straight lines is that they serve as the shortest paths between two points. (i.e., the shortest path between
AandBis given by the line fromAtoB.) while it doesn't make sense to talk about "straight lines" on a sphere, it does make sense to talk about "shortest paths" on a sphere, and that's the "spirit of the law" approach.the "shortest paths" are called geodesics, and on the sphere, these correspond to the largest circles that can be drawn on the surface of the sphere. (e.g., the equator is a geodesic.)
i'm not really sure if the line in question is a geodesic, though
You are absolutely correct, but to add on to that even more:
When we talk about space, we usually think about 3D euclidean space. That means that straight lines are the shortest way between two points, parallel lines stay the same distance forever, and a whole bunch of other nice features.
Another way of thinking about objects like the earth is to think of them as 2D spherical manifolds. That means we concern ourself only to the surface of the earth, with no concept of going below the surface or flying up into the sky. In S2 (that's what you call a 2D spherical manifold), and in spherical geometry in general, parallel straight lines will eventually cross, and further on loop back and form a closed loop. Sounds weird, right? Well, we do it all the time. Look at lines of Longitude, for example.
We call the shortest line connecting two points in curved manifolds geodesics, as you said, and for all intents and purposes, they are straight. Remember, there is no concept of leaving the sphere, these two coordinates is all there is.
What one can do, if one wants to, is embed any manifold into a higher-dimensional euclidean one. Geodesics in the embedded manifold are usually not straight in higher-dimensional euclidean space. Geodesics on a sphere, for example, look like great circles in 3D.
Absolutly fantastic explination of how to conceptualize the complexities of geometry. Such an interesting area of mathematics
What is the slope of a straight line, a linear function? Now what is the slope of a nonlinear function, aka a curved line?
A geodesic would only be accurately labeled a "straight line" IF it was on a plane. On a curved or uneven surface it's a nonlinear function.
https://mathworld.wolfram.com/Geodesic.html#:~:text=A%20geodesic%20is%20a%20locally,circles%20(like%20the%20equator).
i think it depends on what you mean by “accurately”.
from the perspective of someone living on the sphere, a geodesic looks like a straight line, in the sense that if you walk along a geodesic you’ll always be facing the “same direction”. (e.g., if you walk across the equator you’ll end up where you started, facing the exact same direction.)
but you’re right that from the perspective of euclidean geometry, (i.e. if you’re looking at the earth from a satellite), then it’s not a straight line.
one other thing to note is that you can make the “perspective of someone living on the sphere” thing into a rigorous argument. it’s possible to use some advanced tricks to cook up a definition of something that’s basically like “what someone living on the sphere thinks the derivative is”. and from the perspective of someone on the sphere, the “derivative” of a geodesic is 0. so in this sense, the geodesics do have “constant slope”. but there is a ton of hand waving here since the details are super complicated and messy.
this definition of the “derivative” that i mentioned is something that turns out to be very important in things like the theory of general relativity, so it’s not entirely just an arbitrary construction. the relevant concepts are “affine connection” and “parallel transport”, and they’re discussed a little bit on the wikipedia page for geodesics.
Thank you for the informative answer
This whole post is a good illustration to how math is much more creative and flexible than we are lead to believe in school.
The whole concept of "manifolds" is basically that you can take something like a globe, and make atlases out of it. You could look at each map of your town and say that it's wrong since it shouldn't be flat. Maps are really useful, though, so why not use math on maps, even if they are "wrong"? Traveling 3 km east and 4 km north will put you 5 km from where you started, even if those aren't straight lines in a 3d sense.
One way to think about a line being "straight" is if it never has a "turn". If you are walking in a field, and you don't ever turn, you'd say you walked in a straight line. A ship following this path would never turn, and if you traced it's path on an atlas, you would be drawing a straight line on map after map.
I think those last 2 paragraphs are due to people approximating math that would otherwise be quite complex to calculate, or making models that are approximations due to widespread available technology. Just because I don't turn if I cross over Mt Everest, does not mean that is the fastest route by foot.
I'm not saying to not use these approximations.
I really recommend the book "Where Mathematics Comes From," to really think deeply about what math is to us as an animal. Even other animals can do some rudimentary math, and arguably athletes are doing math innately as they perform their sports. Birds and dolphins do physics and calculus. Sort of. In this view, what we teach as math to each other as humans is essentially a language describing these phenomenon and how they work together. Calling this approximation a "straight line" in this language sense isn't very accurate and it's what's causing the debate.
Stop making up bullshit to justify it. It's not a straight line so don't say that it is. Words have meaning.