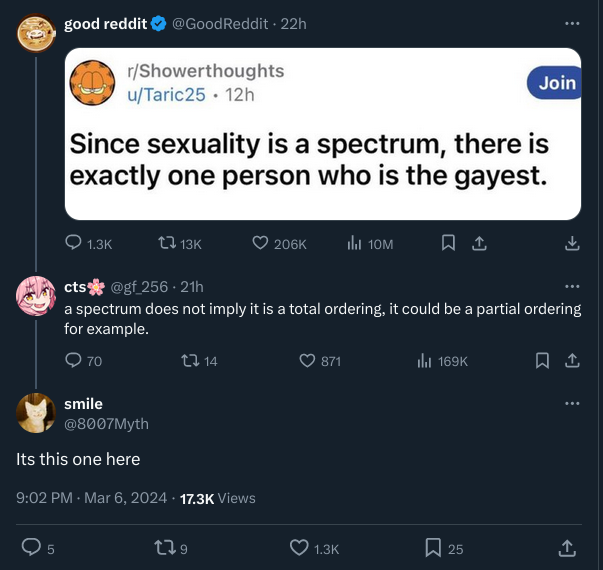
Measure theory gets pretty abstract, so I recommend using a source thats not me. For the Real Numbers, the standard measure (usually the Lebesgue measure) is a way to generalize notions of lengths of intervals to sets that are not intervals or easy unions of intervals. For any set E, we can find various sequences of open intervals (potentially infinitely many intervals) whose union will contain E. The Lebesgue outer measure of E is defined as the infimum of the sum of the lengths of those sequences of intervals (infimum is similar to minimum except that an infimum may not actually be attained). The set E is considered Lebesgue measurable if it satisfies am additional criterion (Caratheodory criterion) in which case the Lebesgue measure is equal to the Lebesgue outer measure. If E does not satisfy that criterion, then it is non-measurable. A measure has desirable certain properties that an outer measure does not satisfy, which is why we prefer the former. Apologies to all math people for any inaccuracies in the above description, it's been a while.